Blog da Professora Ju

“Os primeiros passos são inúteis quando não se percorre o caminho até o fim.” (Shânkara)

Vamos em frente!

Um abraço,
Ju

Olá turminha,
Hoje vou postar um vídeo do professor Márcio Barbosa que encontrei no Youtube. Ele nos mostra uma forma diferente de se aprender a tabuada. Vamos assistir???


Legal né???

Um abraço!
Ju

Olá!!!

Gostaria de agradecer ao seguidor Ziulab pela participação de hoje. Como podem notar, ele está sempre presente. :-) Obrigada!

1 - (TRT/2004)

Vamos analisar uma a uma as pistas dadas no enunciado da questão. Não é necessário seguir a ordem em que as pistas são apresentadas, analise primeiramente as mais fáceis.

1ª pista) TREVO e GLERO não têm letras em comum com ele;
As alternativas que apresentarem as letras T, R, E, V, O, G, L, serão descartadas.
Daí, podemos descartar a alternativa a)
a) MIECA b) PUNCI c) PINAI d) PANCI e) PINCA

2ª pista) PRELO tem uma letra em comum, que está na posição correta;
As alternativas que apresentam somente uma letra em comum com a palavra PRELO, e que está na mesma posição não serão descartadas.
Não há alternativas a serem descartadas!

3ª pista) MUNCA tem com ele três letras comuns, que se encontram na mesma posição;
Podemos descartar as alternativas c) e d)
a) MIECA b) PUNCI c) PINAI d) PANCI e) PINCA

4ª pista) TIROL tem uma letra em comum, que está na posição correta.
Podemos descartar a alternativa b)
a) MIECA b) PUNCI c) PINAI d) PANCI e) PINCA

Portanto, opção correta letra e) PINCA

2 - (TRF/2004)

Relação que existe entre o primeiro grupo de letras (MNAB) e o segundo (MODC):

- A primeira letra do primeiro e do segundo grupo são iguais;
- A segunda letra do primeiro grupo é N e a do segundo grupo é O, são letras que são vizinhas no alfabeto;
- A terceira letra do primeiro grupo é A e a do segundo grupo é D, e no alfabeto há duas letras entre elas;
- A quarta letra do primeiro grupo é B e a do segundo grupo é C, são letras que são vizinhas no alfabeto.

Essas mesmas relações entre as letras do primeiro e do segundo grupos também deverão ocorrer entre as letras do terceiro e quarto grupos.

A alternativa b) será a resposta, veja porque:

(EFRS) - (EGUT)

- A primeira letra do terceiro e do quarto grupo são iguais;
- A segunda letra do terceiro grupo é F e a do quarto grupo é G, são letras que são vizinhas no alfabeto;
- A terceira letra do terceiro grupo é R e a do quarto grupo é U, e no alfabeto há duas letras entre elas;
- A quarta letra do terceiro grupo é S e a do quarto grupo é T, são letras que são vizinhas no alfabeto.

Portanto, a resposta correta é a alternativa b) (EGUT)

3 - (TCE/2005)

O cubo da figura tem três pequenos cubos em cada aresta (altura, largura e comprimento), assim o total de pequenos cubos é igual a 3³, ou seja, 27.

Juntando 8 pequenos cubos podemos formar um outro cubo com 2 pequenos cubos em cada aresta, conforme a figura abaixo:

Agora, temos que observar o cubo fornecido na questão, e tentar visualizar a quantidade de cubos formados com esses pequenos 8 cubos. Podemos visualizar 4 desses cubos na parte inferior e mais 4 desses cubos na parte superior, totalizando 8 cubos.

O cubo formado com os 27 pequenos cubos, também é um cubo, e deve ser considerado na contagem dos cubos visualizados.

Portanto, o número de cubos que podem ser visualizados na figura da questão é:
27 + 8 + 1 = 36 cubos

Alternativa correta letra d)

4 - (OFICIAL JUSTIÇA - SP/1999)

*Questão resolvida pelo professor Vagner Guedes. Obrigada pela colaboração.*

Esta é uma questão fácil, porém necessita uma análise cuidadosa para encontrar o menor caminho. Para irmos de A a B, temos que seguir a ordem imposta na questão: A –> E –> C –> D –> B

Menor distância de A a E: 8 + 3 + 13 = 24
Menor distância de E a C: 13 + 4 = 17
Menor distância de C a D: 4 + 3 = 7
Menor distância de D a B: 3 + 3 + 7 + 5 + 6 = 24

Somando as distâncias obtidas em cada trecho, teremos:
24 + 17 + 7 + 24 = 72

Portanto, resposta correta alternativa e)

OBSERVAÇÃO: No gabarito disponibilizado pela banca examinadora do concurso aparece a alternativa c, ou seja, 70km, com a seguinte solução:

Menor distância de A a E: 8 + 3 + 3 + 9 = 23 
Menor distância de E a C: 9 + 3 + 4 = 16 
Menor distância de C a D: 4 + 3 = 7 
Menor distância de D a B: 3 + 3 + 7 + 5 + 6 = 24

Somando as distâncias obtidas em cada trecho, teremos:
23 + 16 + 7 + 24 = 70

No entanto, assim como o professor Vagner, também concordo que o gabarito esteja errado, pois fazendo este caminho proposto, a ordem das localidades seria A –> D –> E –> D –> C –> D –> B e, portanto, em desacordo com "a ordem" imposta pelo enunciado da questão, que é A –> E –> C –> D –> B.

É isso aí.
Abraços,
Ju

Olá galerinha,

Vamos tentar resolver mais estes probleminhas:

1 - (TRT/2004)

Em relação a um código de cinco letras, sabe-se que:

- TREVO e GLERO não têm letras em comum com ele;
- PRELO tem uma letra em comum, que está na posição correta;
- PARVO, CONTO e SENAL têm, cada um, duas letras comuns com o código, uma que se encontra na mesma posição, a outra não;
- MUNCA tem com ele três letras comuns, que se encontram na mesma posição;
- TIROL tem uma letra em comum, que está na posição correta.

O código a que se refere o enunciado da questão é:

a) MIECA
b) PUNCI
c) PINAI
d) PANCI
e) PINCA

2 - (TRF/2004)

São dados três grupos de 4 letras cada um:

(MNAB) - (MODC) - (EFRS)

Se a ordem alfabética adotada exclui as letras K, W e Y, então o grupo de quatro letras que deve ser colocado à direita do terceiro grupo e que preserva a relação que o segundo tem com o primeiro é:

a) (EHUV)
b) (EGUT)
c) (EGVU)
d) (EHUT)
e) (EHVU)

3 - (TCE/2005)

Considere que o cubo mostrado na figura abaixo foi montado a partir de pequenos cubos avulsos, todos de mesmo tamanho.

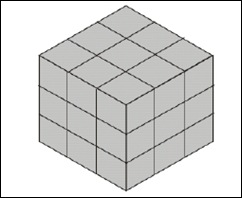
O número de cubos que podem ser visualizados nessa figura é:

a) 9
b) 18
c) 27
d) 36
e) 48

4 - (OFICIAL JUSTIÇA - SP/1999)

O diagrama indica percursos que interligam as cidades A, B, C, D e E, com as distâncias dadas em quilômetros:

 
Partindo-se de A e passando por E, C e D, nessa ordem, a menor distância que poderá ser percorrida para chegar a B é, em quilômetros:

a) 68
b) 69
c) 70
d) 71
e) 72

É isso aí.
Um forte abraço e um ótimo final de semana.
Ju

O que podemos fazer para mudar isso???

Um abraço!
Ju

Olá,

Vamos mostrar como era feita, no ano 830, uma subtração de números inteiros.

Para que você possa acompanhar com facilidade todas as operações, vamos empregar, na representação dos números, algarismos modernos.

Do número 12025 vamos tirar 3604.

A operação era iniciada pela esquerda (operação I). Dizemos: de 12 tirando 3 restam 9; cancelamos os algarismos considerados e escrevemos o resto obtido em cima do minuendo (veja figura abaixo).

Continuamos: de 90 tirando 6 restam 84.

A diferença obtida (operação II) é escrita sobre o minuendo, e os algarismos que formavam os termos da subtração aparecem cancelados.

Finalmente: de 8425 tirando 4 restam 8421 (operação III).

É essa a diferença entre os números dados.

Era assim que Mohamed Ben Musa Alkarismí, geômetra árabe, um dos sábios mais notáveis do Século IX, realizava uma subtração de números inteiros.

Que coisa complicada não?!

Um abraço e até mais.
Ju

Olá turma,

Antes de expor as soluções, gostaria de parabenizar ao seguidor Ziulab pela participação de hoje.
Segue abaixo as respostas:

1 - (BB/1998)

Muito cuidado com este tipo de questão! A resolução da questão é fácil, entretanto, a pergunta é bastante "capciosa", pois pode induzir o candidato ao erro. Senão, vejamos:
a) Com as moedas de 5 centavos, temos o seguinte "engano":
3 * R$ 0,50 - 3 * R$ 0,05 = R$ 1,35;
b) Com as moedas de 1 real, o 'engano' foi o seguinte:
3 * R$ 0,10 - 3 * R$ 1,00 = - R$ 2,70.
Somando-se as duas diferenças encontradas acima:
R$ 1,35 - R$ 2,70 = - R$ 1,35.
Esta é a diferença da quantia INICIAL em relação à CORRETA, ou seja, a partir da quantia INICIAL, deve-se ACRESCENTAR R$ 1,35 para se chegar à quantia CORRETA.

(Opção correta letra A)

2 - (PRF/1998)

Se o relógio de João adianta 20 s por dia e o relógio de Maria atrasa 16 s por dia, então, a cada dia, seus relógios apresentarão uma diferença de 20 + 16 = 36 s. Ora, a diferença total entre os dois relógios, após X dias, era, em segundos, de 4 * 60 + 30 = 270 s. Para encontrarmos o número de dias necessários para perfazer esta diferença, basta dividirmos a diferença total (270) pela diferença diária (36). Encontraremos 7,5 (sete dias e meio, ou seja, sete dias mais doze horas). Somando-se 7 dias a partir do dia 7 de março, iremos para o dia 14 de março. Entretanto, ao somarmos as 12 horas (meio dia) com a hora em que os relógios foram acertados (14 horas), iremos ultrapassar as 24 horas do dia 14, indo para 2h da manhã do dia 15 de março.

(Opção correta letra E)

3 - (TRT/2001)

15⁸ = (3 * 5)⁸ = 3⁸ * 5⁸;
No conjunto dado, sabe-se que:
81 = 3⁴, que é divisor de 3⁸ * 5⁸;
125 = 5³, que também é divisor de 3⁸ * 5⁸;
225 = 3² * 5², que também é divisor de 3⁸ * 5⁸;
já o nº 250, quando decomposto em fatores primos, possui o fator “2”, ou seja: 250 = 2 * 5³.
Ora, o fator 2 NÃO É DIVISOR de 3⁸ * 5⁸, logo, encontramos o número procurado (aquele que não é divisor de 15⁸.
Apenas complementando o raciocínio:
405 = 3⁴ * 5 , cujos fatores também são divisores de 15⁸.

(Opção correta letra D)

4 - (CEF/2004)

Para a primeira divisão temos:
⇒ P(1) = 2 (equação I)

Para a segunda divisão temos:
⇒ P(3) = 4 (equação II)

O resto da divisão de P(x) por (x - 1).(x - 3) é do tipo: R(x) = ax + b, pois gr (D) = 2 (grau do divisor é dois).
Observe que x² − 4x + 3 = (x−1).(x−3)

Da definição de divisão temos:
⇒ P(x) ≡ (x - 1).(x - 3).Q(x) + ax + b (equação III)

Na equação III, quando x = 1 e x = 3, temos:
a) para x = 1 ⇒ P(1) = (1 - 1).(1 - 3).Q(x) + a.1 + b ⇒ 2 = a + b
b) para x = 3 ⇒ P(3) = (3 - 1).(3 - 3).Q(x) + a.3 + b ⇒ 4 = 3.a + b

Disto resultou o seguinte sistema:
a + b = 2
3a + b = 4

Resolvendo-se pelo método da adição, após multiplicar a primeira equação por
(-1), temos:
-a -b = -2
3a + b = 4
Logo, 2a = 2 ⇒ a = 1.

Substituindo-se este resultado na primeira equação, vem: b = 1. Disto resulta o resto procurado: x + 1.

(Opção correta letra B)

Abraços,
Ju

Olá pessoal,

Continunado o tópico “questões de concursos” vou deixar para vocês mais quatro questões. Vamos tentar resolvê-las???

1 - (BB/1998)

Ao receber moedas como parte de um pagamento, um caixa de uma agência bancária contou t moedas de 1 real, y de 50 centavos, z de 10 centavos e w de 5 centavos. Ao conferir o total, percebeu que havia cometido um engano: contara 3 das moedas de 5 centavos como sendo de 50 centavos e 3 das moedas de 1 real como sendo de 10 centavos. Nessas condições, a quantia correta é igual à inicial

a) acrescida de R$ 1,35
b) diminuída de R$ 1,35
c) acrescida de R$ 1,65
d) diminuída de R$ 1,75
e) acrescida de R$ 1,75

2 - (PRF/1998)

João e Maria acertaram seus relógios às 14 horas do dia 7 de março. O relógio de João adianta 20 s por dia e o de Maria atrasa 16 s por dia. Dias depois, João e Maria se encontraram e notaram uma diferença de 4 minutos e 30 segundos entre os horários que seus relógios marcavam. Em que dia e hora eles se encontraram?

a) Em 12/03 à meia noite
b) Em 13/03 ao meio dia
c) Em 14/03 às 14 h
d) Em 14/03 às 22 h
e) Em 15/03 às 2 h

3 - (TRT/2001)

Dentre os números 81, 125, 225, 250 e 405, o único que não é divisor de 15⁸ é:

a) 81
b) 125
c) 225
d) 250
e) 405

4 - (CEF/2004)

Dividindo o polinômio P(x) por x - 1, tem-se para resto 2; dividindo-o por x - 3, o resto é 4. O resto do polinômio P(x) por x² - 4x + 3 é:

a) 1 - 4x
b) x + 1
c) -4x + 4
d) x - 4
e) x + 3

É isso aí. Vou ficando por aqui. Qualquer dúvida, é só perguntar.

Um abraço e um ótimo final de semana.
Ju

"A essência da matemática não é para fazer das coisas simples, complicadas, mas para tornar as coisas complicadas simples."
(S. Gudder)

Um abraço!
Ju

Olá galerinha,

Finalizando as postagens sobre a origem de alguns sinais matemáticos, hoje vamos conhecer como surgiram os sinais de relação (>, < e =).

Roberto Record, matemático inglês, terá sempre o seu nome apontado na história da Matemática por ter sido o primeiro a empregar o sinal = (igual) para indicar igualdade. No seu primeiro livro, publicado em 1540, Record colocava o símbolo entre duas expressões iguais; o sinal =, constituído por dois pequenos traços paralelos, só apareceu em 1557. Comentam alguns autores que nos manuscritos da Idade Média o sinal = aparece como uma abreviatura da palavra est.
Guilherme Xulander, matemático alemão, indicava a igualdade, em fins do século XVI, por dois pequenos traços paralelos verticais; até então a palavra aequalis aparecia, por extenso, ligando os dois membros da igualdade.
Os sinais > (maior que) e < (menor que) são devidos a Thomaz Harriot, que muito contribuiu com seus trabalhos para o desenvolvimento da análise algébrica.

Texto extraído do livro “Matemática divertida e curiosa” do autor Malba Tahan.

Clique sobre os nomes se quiser conhecer a origem dos sinais de soma e subtração e a origem dos sinais de multiplicação e divisão.

Abraçosssss!
Ju

Olááá pessoal,

Primeiramente, gostaria de agradecer aos dois pariticpantes: Ziulab e Marcos Rogério. Obrigada. :-)

Eis as soluções:

1 - (MPU/2007)

Seja x o número de funcionários presentes na reunião. Portanto temos (x+1) pessoas presentes na reunião (x funcionários + o presidente). O presidente retirou o primeiro salgadinho. Então, sobraram 27 salgadinhos que serão divididos entre os funcionários e o presidente. Como a mesa é circular a bandeja passa várias vezes em torno dela. A cada volta da bandeja em torno da mesa são retirados (x+1) salgadinhos. Como o presidente retirou o último salgadinho temos que (x+1) é um divisor de 27. Então, os valores possíveis para (x+1) são 1,3,9,27. Logo, o total de participantes dessa reunião (x+1) só pode ser 9, conforme as alternativas.

(Opção correta letra B)

2 - (TRF/2001)

Some 1 ao anterior, e depois multiplique o anterior por três alternadamente.

Veja:

1) 0 = 0
2) 0+1 = 1
3) 1x3 = 3
4) 3+1 = 4
5) 4x3 = 12
6) 12+1 = 13
7) 13x3 = 39
8) 39+1 = 40
9) 40x3 = 120
10) 120+1=121

A soma do oitavo com o décimo será 40 + 121 = 161

(Opção correta letra A)

3 - (TRT/2001)

Vamos decompor os números dados em fatores primos: 400 = 2⁴  x 5² ; 500 = 2² x 5³ ; 1250 = 2 x 5⁴.
Para que um número natural seja divisível pelos 3 números decompostos acima, deverá ser um múltiplo comum destes, ou seja: MMC (400, 500, 1250) = 2⁴  x 5⁴ = 10⁴

(Opção correta letra D)

4 - (TCU/1995)

Vamos assumir que existem “x” candidatos do sexo masculino e “y” candidatos do sexo feminino.
Considerando-se também que a soma das idades de todos os candidatos do sexo masculino seja ΣX e a soma das idades de todos os candidatos do sexo feminino seja ΣY. Com essas considerações, podemos escrever a seguinte equação:

ΣX + ΣY / x + y = 36

Sabemos ainda que, quando separados por sexo:

ΣX / x = 37 e ΣY / y = 34

Isolando-se ΣX e ΣY nas duas últimas equações, temos:

ΣX = 37x e ΣY = 34y

Agora, vamos substituir esses dois resultados na primeira equação:

37x + 34y / x + y = 36 ⇒ 37x + 34y = 36(x + y) ⇒ 37x + 34y = 36x + 36y ⇒ (isolando-se o “x” no primeiro membro e o “y” no segundo) ⇒ 37x - 36x = 36y - 34y ⇒ x = 2y

O problema solicitou o cálculo da razão entre o número de homens e mulheres ou seja, a razão entre “x” e “y”, logo,  x / y = 2

(Opção correta letra C)

Abraços!
Ju

Olá pessoal,

Você já parou para pensar que hoje em dia é moda prestar concurso público? Pare e pense: com certeza você tem na família algum “concurseiro” de plantão. Atualmente, a maioria dos jovens já entra na faculdade, seja lá qual curso for, sonhando com um crachá pendurado no pescoço do TCU, da Receita Federal, ou algum outro “órgão dos sonhos”. Claro, hoje,  o mercado de trabalho está saturado com um grande número de novos profissionais que se formam todo ano. A instablidade, essa aterrozrizante palavrinha, é outra grande causa que leva milhares de pessoas a sonharem com uma vaguinha pública, e, por fim, os altos salários, principlamente, quando comparamos os salários iniciais para uma mesma instrução.

Considerando que os posts que tiveram maior acesso no blog foram os que trouxeram questões de concursos e, sobretudo, para atender este nicho de estudantes, postarei nos próximos Enigmas da Ju questões que já cairam em concursos públicos passados. A metodologia continuará a mesma, na sexta-feira, postarei algumas questões, e, na terça, publicarei as respostas. Espero que gostem. :-) Ahh, mas para quem não tem interesse em concursos, pode tentar resolver as questões também, continuarei postando os nomes dos participantes. :-)

1 - (MPU/2007)

Ao longo de uma reunião, da qual participaram o presidente de certa empresa e alguns funcionários, foram servidos 28 salgadinhos em uma bandeja. Sabe-se que:

– todos os participantes da reunião sentaram-se ao redor de uma mesa circular;
– o primeiro a ser servido dos salgadinhos foi o presidente e, após ele, sucessivamente, todos os demais também o foram, um a um, a partir da direita do presidente;
– a cada passagem da bandeja, todas as pessoas se serviram, cada qual de um único salgadinho;
– coube ao presidente ser servido do último salgadinho da bandeja.

Considerando que as pessoas podem ter comido mais de um salgadinho, o total de participantes dessa reunião poderia ser:

(A) 4
(B) 9
(C) 10
(D) 13
(E) 15

2 - (TRF/2001)

Considere que os termos da sucessão (0, 1, 3, 4, 12, 13, ...) obedecem a uma lei de formação. Somando o oitavo e o décimo termos dessa sucessão obtém-se um número compreendido entre:

(A) 150 e 170
(B) 130 e 150
(C) 110 e 130
(D) 90 e 110
(E) 70 e 90

3 - (TRT/2001)

O menor número natural, não-nulo, que é divisível por 400, 500 e 1250 é:

a) 10²
b) 10³
c) 5*10³
d) 10⁴
e) 10⁵

4 - (TCU/1995)

A média aritmética das idades dos candidatos a um concurso público federal é de 36 anos. Quando separados por sexo, essa média é de 37 anos para o grupo do sexo masculino e 34 para o grupo do sexo feminino. A razão entre o número de homens e mulheres é:

a) 1/2
b) 37/34
c) 2
d) 34/37
e) 36/34

Tente resolver aí, terça-feira postarei as soluções.

Um abraço e um ótimo final de semana.
Ju

Olááá,

Tradução: "Como eu posso confiar na sua informação quando você usa esta tecnologia ultrapassada?"

Nada contra os computadores, muito pelo contrário, eles são ótimos. Fazem de tudo… e tudo muito rápido! No entanto, ainda acredito que o uso do giz (tudo bem, vamos modernizar um pouquinho, da caneta esferográfica)  e do quadro são provas de que estamos realmente interagindo com as pessoas, e não fazendo download em massa de conteúdos para um vestibular platônico. A caneta está ali, livre em sua simplicidade, pronta para responder a qualquer ideia maluca que venha do professor ou dos alunos. Ou uma dúvida mais complexa, um comentário interessante. Com esta simples ferramenta, a cultura pode ser criada ao vivo, na frente dos alunos, interagindo de fato com eles. Enfim, ainda acredito que, por trás disso tudo, existe um ser humano que continua se esforçando para ser humano. Até quando eu não sei…

Fico por aqui.

Abraços,
Ju

Olá galerinha,

Dando continuidade à série origem dos sinais matemáticos, hoje vamos conhecer um pouquinho sobre os sinais de multiplicação e divisão. Vamos lá???

Origem do sinal de multiplicação:

O sinal x, com que indicamos a multiplicação, é relativamente moderno. O matemático inglês Guilherme Oughtred, empregou-o, pela primeira vez, no livro Clavis Matematicae publicado em 1631. Ainda nesse mesmo ano, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores.
Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Na obra de Leibniz encontra-se o sinal   para indicar multiplicação; esse mesmo símbolo colocado de modo inverso indicava divisão.

Origem do sinal de divisão:

As formas a/b e , indicando a divisão de a por b são atribuídas  aos árabes; Oughtred, em 1631, colocava um ponto entre  o dividendo e o divisor.
A razão entre duas quantidades é indicada pelo sinal :, que  apareceu em 1657 numa obra de Oughtred. O sinal ÷ segundo Rouse Bali, resultou de uma combinação de dois sinais existentes - e :.

Texto extraído do livro “Matemática divertida e curiosa” do autor Malba Tahan. Grifo meu.

Clique aqui para conhecer a origem dos sinais de soma e subtração.

Na próxima semana postarei sobre a origem dos sinais de relação (=, > e <). Apareçam!

Bjinhos,
Ju

Oláááá pessoal,

Poxa, o que houve com as participações??? Todo mundo sumiu…:-( 
O probleminha estava muito difícil ou foi o feriadão prolongado, a segundona preguiçosa que fez todo mundo desaparecer???

Não poderia deixar de agradecer e parabenizar o único participante: Ziulab. Muito obrigada!

Vamos a solução:

Para resolver o enigma, vamos utilizar o princípio do valor posicional dos algarismos, por exemplo, 72 = 10*7 + 2

Analogamente, podemos escrever:

xy = 10x + y

Logo,

yx = 10y + x

Também, é fato que:

x0y = 100x + 0*10 + y*1 = 100x + y

Obs.: por exemplo, 203 = 100*2 + 0*10 + 3*1

Sabemos que a velocidade é igual à distância percorrida dividida pelo intervalo de tempo (v = d/t). Como os intervalos de tempo são unitários (1 h), teremos que, numericamente, v = d.

A distância percorrida na primeira hora (entre 13 e 14:00h) foi igual a:

d = (10y + x) - (10x + y) = 9y - 9x

A distância percorrida na segunda hora (entre 14 e 15:00h) foi igual a:

d = (100x + y) - (10y + x) = 99x - 9y

Como a velocidade é constante, teremos, já que neste caso, a velocidade é numericamente igual à distância:

99x - 9y = 9y - 9x

9(11x - y) = 9(y - x)

11x - y = y - x

11x + x = y + y

12x = 2y, logo y = 6x

Lembrando que x e y são necessariamente inteiros e positivos menores ou iguais a 9, pois os números xy e yx possuem dois algarismos cada, concluímos que o único valor possível para x é 1, o que implica y = 6.

Logo, o primeiro marco foi 16, o segundo 61 e o terceiro 106.

Ora, se o veículo passou no km 16 e após 1h, passou no km 61, ele percorreu 45 km em uma hora e, portanto, a sua velocidade era de 45 km/h.

Como o problema pede a velocidade em m/s - metros por segundo - vem:

V = 45 km/h = 45000m/3600s = 450/36 = 12,5 m/s

É isso aí, vou ficando por aqui.

Um abraço!
Ju

Olá pessoal,

Vamos tentar resolver mais um probleminha???

Paulinho estava viajando a uma velocidade constante por uma estrada, em companhia de seu pai Roberto e sua mãe Ana. Como o velocímetro estava com defeito, Roberto solicitou ao Paulinho que fizesse algumas anotações com o objetivo de calcular a velocidade desenvolvida pelo veículo durante o percurso.

Paulinho efetuou as seguintes anotações:

1 - Às 13:00h, meu pai passou num ponto cujo marco da quilometragem, não consegui anotar. Entretanto, tenho certeza que o marco indicava dois algarismos.

2 - Às 14:00h, meu pai passou em outro ponto e, num relance, percebi que o marco indicava os mesmos algarismos, porém numa ordem invertida.

3 - Intrigado com a coincidência, resolvi anotar a quilometragem do próximo marco, decorridos mais uma hora. Tive então, a surpresa de perceber que o marco indicava os algarismos observados às 13:00h, porém, com um zero intercalado entre eles.

Nestas condições, qual era velocidade do veículo em metros por segundo?

Para quem já se esqueceu: V=d/t, onde V=velocidade, d=distância percorrida e t=tempo.

Tente resolver aí. Terça-feira postarei a solução.

Um abraço e um ótimo final de semana.
Ju

Qual o caminho para tornar a matemática mais fascinante???

A Matemática sempre foi vista como a matéria aterrorizadora dos alunos. Quando se pergunta nas escolas qual a disciplina que os alunos mais gostam, aparecem com maior frequência a Língua Portuguesa, Ciências, Geografia e História, sendo que a Matemática é a menos citada na grande maioria das vezes. 

Por que será que isso acontece?

Sabe-se que os seres humanos nascem com habilidades múltiplas e alguns possuem habilidades mais aguçadas para determinadas áreas. Os que tendem à área de exatas se dão muito bem na escola com a matemática, física ou química. Já outros, precisam desenvolver essas habilidades e é neste ponto que entra a importância do “como” desenvolvê-las.

A criança enquanto na educação Infantil, e até mesmo nas séries iniciais, possui um contato maior com atividades lúdicas, porém, isso vai se perdendo no decorrer dos anos. Este fato faz com que os alunos conscientizem-se do material lúdico como ferramenta voltada apenas para “crianças” e quando estão já no fundamental II ou no ensino médio, acreditam que não precisam mais dar passos por este valioso caminho.

Outro motivo é a forma como são introduzidos tais materiais. Um exemplo é o trabalho com os blocos lógicos. Na Educação infantil, muitas vezes os professores restringem-se apenas a deixar os alunos “brincarem” com o material, montando casinhas, carrinhos e robozinhos e perdem o foco do trabalho com este material. Às vezes até trabalham a questão das formas geométricas, porém estagnam.

Quando esses alunos chegam no 1º, 2º ano não querem mais trabalhar com os blocos, pois acham que são só pra “criancinhas”. Para que tal fato não ocorra, o professor deve deixar bem claro aos alunos a importância desse material, traçando assim seus objetivos, mesmo que não trabalhe com todas as possibilidades.

Só para ressaltar, com os blocos lógicos é possível trabalhar no fundamental II ou até mesmo no ensino médio, fazendo um Jogo de Dominós, utilizando todas suas características e propriedades.

E por que não ensinar a função seno aos alunos do ensino médio com a ajuda de rodas de carro e uma vara de pescar? E a função quadrática, que tal levar os alunos em um jogo de voleibol para entenderem o que é uma parábola?

Esse é o caminho, utilizar materiais concretos e do cotidiano para explicar conteúdos tão abstratos aos alunos.

A partir do momento que o aluno tomar consciência de que a matemática pode ser entendida e não só decorada; encontrada ao seu redor e não como algo vindo do além (abstrato) pode-se mudar esse quadro e encontrar com mais frequência a resposta MATEMÁTICA para a pergunta: qual a matéria que você mais gosta?

Pense nisso…

Um abraço!
Ju

Oláááá,

Você saberia dizer de onde surgiu o + (mais ) e o - (menos) que escrevemos em todas as operações de soma e subtração que realizamos. Na escola, aprendemos que para somar temos que utilizar o sinal de mais (+) e para subtrair o sinal de menos (-), no entanto, pouco se fala da origem desses sinais. Vamos conhecer um pouquinho sobre eles???

Origem do sinal de adição:

O emprego regular do sinal + (mais) aparece na Aritmética Comercial de João Widman d’Eger publicada em Leipzig em 1489.
Os antigos matemáticos gregos, como se observa na obra de Diofanto, limitavam-se a indicar a adição justapondo as parcelas – sistema que ainda hoje adotamos quando queremos indicar a soma de um número inteiro com uma fração. Como sinal de operação mais usavam os algebristas italianos a letra P, inicial da palavra latina plus.

Origem do sinal de subtração:

É interessante observar as diferentes formas por que passou o sinal de subtração e as diversas letras de que os matemáticos se utilizaram para indicar a diferença entre dois elementos.
Na obra de Diofanto, entre as abreviaturas que constituíam a linguagem algébrica desse autor,encontra-se a letra grega ψ indicando subtração. Essa letra era empregada pelo famoso geômetra de Alexandria como sinal de operação invertida e truncada.
Para os hindus – como se encontra, na obra de Bhaskara – o sinal de subtração consistia num simples ponto colocado sob o coeficiente do termo que servia de subtraendo.
A letra M – e, às vezes, também m – foi empregada, durante um longo período, para indicar a subtração, pelos algebristas italianos. Luca Pacioli, além de empregar a letra m, colocava entre os termos de subtração a expressão DE, abreviatura de demptus.
Aos alemães devemos a introdução do sinal - (menos), atribuído a Widman. Pensam alguns autores que o símbolo - (menos), tão vulgarizado e tão simples, corresponde a uma forma limite para a qual tenderia a letra m quando escrita rapidamente. Aliás, Viète – considerado como fundador da Álgebra moderna – escrevia o sinal = entre duas quantidades quando queria indicar a diferença entre elas.

Texto extraído do livro “Matemática divertida e curiosa” do autor Malba Tahan - pseudônimo de Júlio César de Mello e Souza.

É isso aí. Na próxima semana, postarei sobre a origem dos sinais de multiplicação e divisão.

Um abraço!
Ju