Bom, se quiser, pode - estamos num país livre. Supostamente. Mas isso não vai lhe dar a resposta certa.
Na escola, aprendemos uma maneira fácil de multiplicar frações: basta multiplicarmos os números de cima (os numeradores) e os de baixo (os denominadores), assim:
Mas a regra para somá-las é muito mais complicada. “Coloque-as sobre um denominador comum (o número de baixo), depois some os numeradores (os números de cima)”. Porque não podemos somá-las da mesma maneira? Porque está errado? E o que devemos fazer em vez disso?
A resposta curta é que não podemos somar frações dessa maneira porque não vamos encontrar a resposta certa! Como é quase igual a
, e o mesmo vale para
, quando somamos essas frações, o resultado deve ser no mínimo
. Mas
é menor que
, porque metade de 12 é 6. O erro é ainda mais evidente quando tentamos somar
, porque
, não faz sentido: como
, isto seria o mesmo que dizer que
.
Tudo muito bem, mas por que a regra da multiplicação funciona, e o que devemos usar para a adição?
A maneira mais fácil de enxergarmos por que as regras são diferentes - como devem ser - é usando figuras. Eis uma figura para .
A barra vertical mostra uma linha com cinco pedaços iguais, dos quais dois foram pintados de laranja. Isso representa : duas partes de cinco. Da mesma forma, a barra horizontal representa
. Os retângulos representam a multiplicação, porque a área do retângulo é o que obtemos quando multiplicamos os dois lados. O retângulo grande contêm
quadrados. O retângulo laranja contêm
quadrados. Portanto, o retângulo laranja é
do retângulo grande.
Quando estamos somando, a figura correspondente é a seguinte:
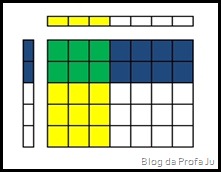
do retângulo grande pegando as duas primeiras fileiras dentre as cinco, e
pegando as três colunas da esquerda dentre as sete. Estas regiões estão mostradas na figura acima, nas cores em amarelo, azul e verde. A cor verde é para indicar a sobreposição das regiões.
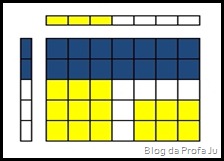
Para contar quantos quadrados existem no total, temos de contar os quadrados sobrepostos duas vezes, ou então, fazer uma cópia adicional, como na figura abaixo.
De qualquer forma, ficamos com 29 quadrados dentre 35, portanto, a soma deve ser .
Para entender como o 29 se relaciona com os números originais basta contarmos os quadrados das duas fileiras, , e somá-los aos das três colunas à esquerda,
. Então,
. Portanto, a regra da adição é
.
É daí que vem a receita habitual “coloque as duas frações sobre o mesmo denominador”.
Referência: Incríveis Passatempos Matemáticos, do autor Ian Stewart, editora Zahar.
Vou ficando por aí.
Grande abraço,
Ju






























25 de abril de 2011 às 20:23
Olá, profa Ju!
Grande! Ótima postagem! Realmente, é o tipo da coisa que se deve fazer para que... não reste a menor dúvida, quando se tenta ensinar a alguém essas operações matemáticas! Uma visão gráfica ( geométrica ) sobre o que queremos ensinar é muito proveitosa! Meus parabéns e... vamos continuar assim!
Um abraço!!!!!