Blog da Professora Ju

Olá pessoal,

Dando continuidade as técnicas de multiplicação de dois números naturais, hoje vamos conhecer um pouquinho do método indiano.

Está preparado???

Os matemáticos hindus desenvolveram um método de multiplicação através de tábuas quadriculadas. Mais tarde os árabes o levaram para a Europa e ficou conhecido como Método da Gelosia.

Para ficar mais fácil entender este método, vamos simplificar e explicá-lo através de um exemplo, ok???

Exemplo 1:

Multiplicar 6538 por 547

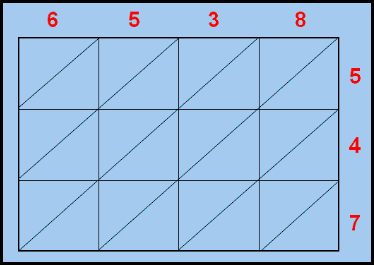
Inicialmente eles construíam uma tabela com 4 colunas e 3 linhas, por conta da quantidade de algarismos dos números envolvidos na operação.

Vejamos como ficava essa tabela.

Traçamos as diagonais desses quadradinhos, como mostramos abaixo:

Dentro de cada quadradinho colocamos os resultados das multiplicações dos algarismos correspondentes da coluna e da linha. Se o resultado for de apenas um dígito deve ser escrito precedido de zero.

Em seguida somamos os algarismos que estão nas mesmas diagonais. Usamos a mesma técnica do “vai um “ que usamos no algoritmo tradicional. Vejamos:

 
Podemos então concluir que o resultado da multiplicação proposta é:

6538 x 547 = 3576286

Ainda está com dúvida??? Que tal um outro exemplo???

Exemplo 2:

Multiplicar 537 por 24

Logo, 537 x 24 = 12888

Mas por que será que funciona?

Para justificarmos o método, devemos lembrar que, na multiplicação 537 x 24, temos na realidade (500 + 30 + 7) x (20 + 4). Se aplicarmos a propriedade distributiva, teremos:

Verifique que as somas que obtivemos em cada coluna são exatamente iguais às somas das diagonais do método da Gelosia. Isso nos mostra que os antigos hindus já conheciam o valor posicional dos algarismos no sistema de numeração decimal.

Texto extraído do livro “A Magia da Matemática”, da Editora Ciência Moderna.

Se quiser conhecer as outras técnicas de multiplicação já postadas no blog clique em cima dos nomes: Multiplicação Russa e Multiplicação Egípcia.

Na próxima semana postarei a técnica chinesa. Apareçam!

Um abraço!
Ju